W poprzednich odcinkach przyjrzeliśmy się ogólnemu cyklowi życia modelu językowego (trenowanie i inferencja) oraz temu, jak modele “rozumieją” (a raczej: przetwarzają) język naturalny w oparciu o semantykę, atencję i tensory. Teraz kontynuujemy, zagłębiając się w technikalia 🥩.
‐ Mówiłeś, że fizycznie model jest zestawem liczb (razem z metadanymi). I to jest ta wiedza modelu?
‐ Dokładnie tak. Przy czym różne macierze/wektory reprezentują inne kawałki, powstałe wskutek treningu.
‐ Będzie matematyka?
‐ Troszeczkę. Luz 😉
“Wiedza” modelu
Podczas treningu kalibrujemy m.in. te wspominane wielokrotnie tensory.
One są, nazwijmy to, “nietypową” reprezentacją stanu “wiedzy” modelu.
Ale nie myśl o wiedzy ani jako o “tekście” (bo przecież model NIE operuje bezpośrednio na tekście tylko na wektorach liczb). Nie myśl też o wiedzy jako o zbiorze “faktów” – bo tego model też nie potrafi przetwarzać.
Wyobraź sobie, że Twoja “zinternalizowana” reprezentacja “jabłka” (odwołując się do wcześniejszego przykładu) jest bardzo mocno rozproszona (“rozsmarowana”) po potencjalnie wszystkich neuronach w Twoim mózgu. I że nie masz tam “faktów” o jabłku, ale raczej pewne “wzorce” połączeń (synaptycznych) – które w określonych okolicznościach mogą się “aktywować” i prowadzić do określonych skojarzeń i interpretacji.
Matematycznie, w wielowymiarowej przestrzeni, jesteśmy w stanie obliczać “bliskość” wielowymiarowych wektorów do/od siebie.
I to właśnie dzieje się w środku modelu (między innymi). Na gigantyczną skalę.
‐ No dobrze, ale kiedy ja piszę prompta, to przecież piszę tekst, a nie liczby. Mówisz, że model nie operuje na tekście – to na czym?
‐ Na wektorach liczb. I to jest właśnie klucz do zrozumienia, jak modele językowe “procesują”. Ale owszem, “na wejściu” model dostaje tekst (prompt w takiej czy śmakiej formie). Ale ten tekst jest natychmiast “tłumaczony” na wektory liczb – i to na nich model operuje.
‐ Tłumaczy tekst na liczby? 🤔
Z tekstu na wektory
Każdy model ma swój własny język, słownictwo, zwał jak zwał. Każdy model – inny. Dlatego wektory wewn. jednego modelu – i drugiego – mają się niejako do siebie, jak pięść do nosa.
Kiedy LLM “dostaje na wejściu” tekst (prompt) – to ów tekst jest najpierw
- tokenizowany, a potem
- embeddowany (“osadzany” w modelu, czyli zamieniany na wektory liczb – ale wektory pobrane właśnie ze słownika tego modelu).
Sęk w tym, że każdy wytrenowany model (model w konkretnej wersji i konkretnej kwantyzacji) ma ten słownik inny.
To trochę tak, jakbym powiedział “Cały dzień biegałem z taczką i przewoziłem piasek“. Jakie będą skojarzenia? Mimo że wszyscy mówimy po polsku, to pierwsze skojarzenie (punkt startowy, zanim zaczniemy dalej internalizować znaczenie tekstu) będzie inne dla każdego z nas.
Tokenizacja
Podczas treningu, oprócz wielu innych rzeczy, model “uczy się” rozcinać tekst na kawałki – tokeny:

(przykładowy tokenizer – niektóre są dołączane do modeli, inne są “standalone”)
Tokeny są potem przetwarzane zarówno osobno jak i wspólnie:
- osobno – bo każdy token ma swoją osobną reprezentację (która nota bene jest częścią modelu, choć relatywnie bardzo małą w porównaniu do reszty – od kilku procent do poniżej 1% całości)
- wspólnie – bo model “patrzy” na sekwencje tokenów, a także szuka powiązań między nimi (to dokładnie robi atencja). Np. w zdaniu “Jabłko spadło na ziemię. Później je zjadłem. Było smaczne” – czego dotyczy “było smaczne”? Jabłka, prawda?
I właśnie to przetwarzanie (osobno i wspólnie) dzieję się właśnie na kartach graficznych GPU 🤓, bo tam te obliczenia są niesamowicie szybkie.
Tylko znowu…

My, ludzie, myślimy o zdaniu np. kluczem gramatyki:
- “jabłko” – przedmiot
- “było smaczne” – obserwacja dotycząca przedmiotu
Model – po pierwsze nie słowami, tylko ich cząstkami (tokenami). ALE… po drugie – nie tokenami jako takimi (bo to były znaki – a te niekoniecznie przetwarzałoby się wydajnie na dużą skalę – procesory najlepiej przecież umieją w operacje na bitach i bajatch)… więc trzeba teraz tokeny “przeflancować” na wektory liczb.
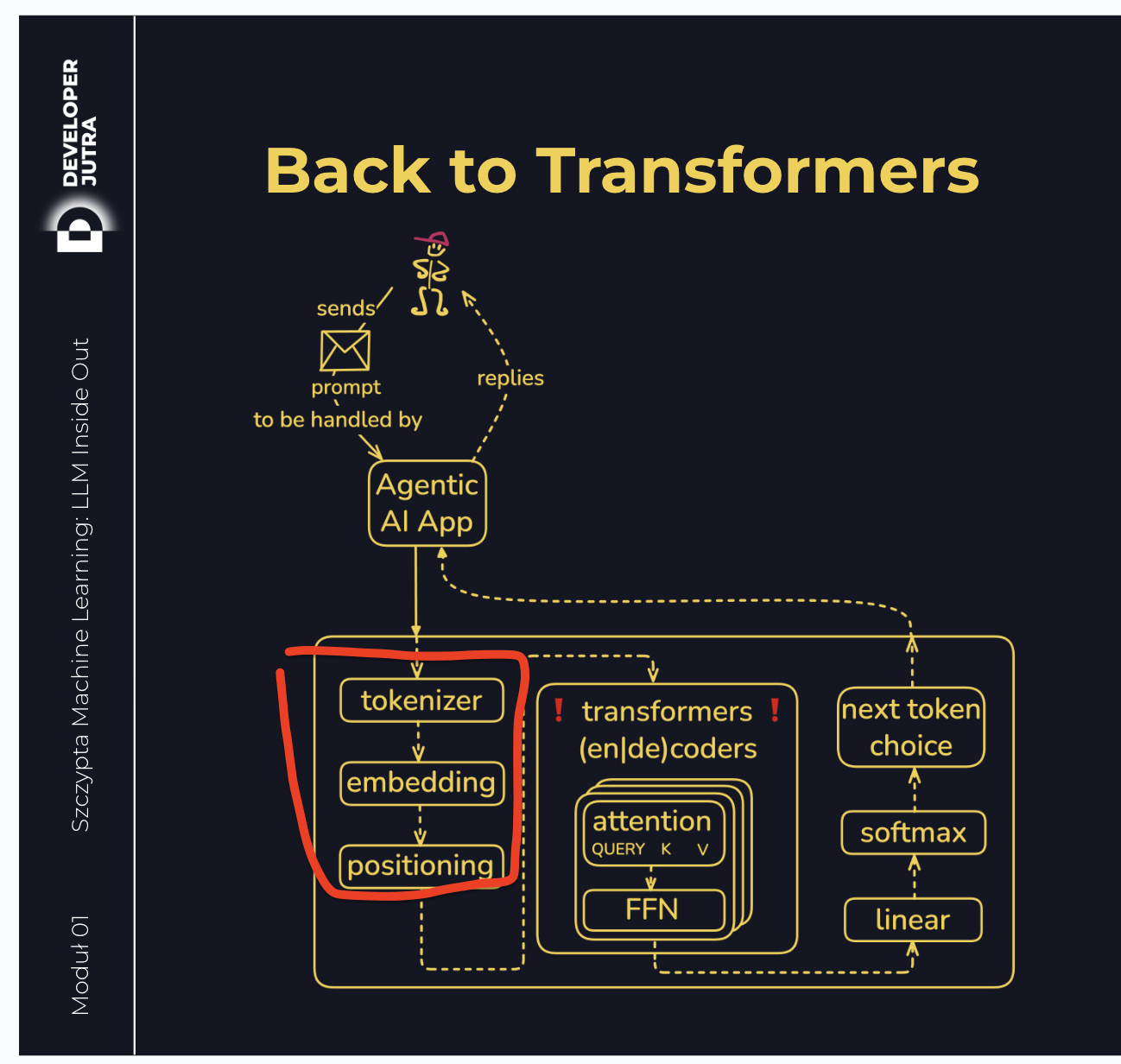
Jesteśmy tu:
Token “Ca“ (z “Cały dzień …“, zdanie powyżej) “otrzymuje” przypisane mu ID: 30942. I to 30942 w innych modelach może oznaczać coś zupełnie innego (i b. często dokładnie tak jest), bo zwyczajnie proces treningu przebiegał inaczej.

A zatem: “Cały dzień biegałem z taczką i przewoziłem piasek“. Jakie będą skojarzenia?
- Dla jednego: “a po co? nie możesz kogoś wynająć”
- Dla drugiego: “praca fizyczna jest super”
- Dla trzeciego: “co mnie to obchodzi?”
- A dla czwartego: “W 1969r. też miałem taczkę…”.
I tak dalej.
Wskutek treningu modelu, ten wykształcił (skalibrował 😄) sobie swój własny “słownik”, który mapuje tokeny na… IDki 😛
Embedding
Następnie, następuje embedding, czyli “osadzenie” tokenów (wg IDka) w przestrzeni wektorowej.

Zaczyna sie matematyka 🤓.
ID 30942 (token “Ca”) ma swój wpis w macierzy po lewej (macierzy embeddingów). Technicznie – wchodzi do słownika pod konkretny klucz i bierze wektor 😊 O jakiej długości? Takiej jak długość embeddingu danego modelu. W przypadku Bielika (ilustracja poniżej): 4096 (potęga dwójki – ciekawe czemu 🤔😅)
‐ Whoa, ale jazda 🤯
‐ Noo, a to dopiero początek początków 😉
Teraz możemy majestatycznie zedrzeć fasadę magii i tajemnicy tych różnych liczb, określanych m.in. przez “parametry modelu”.
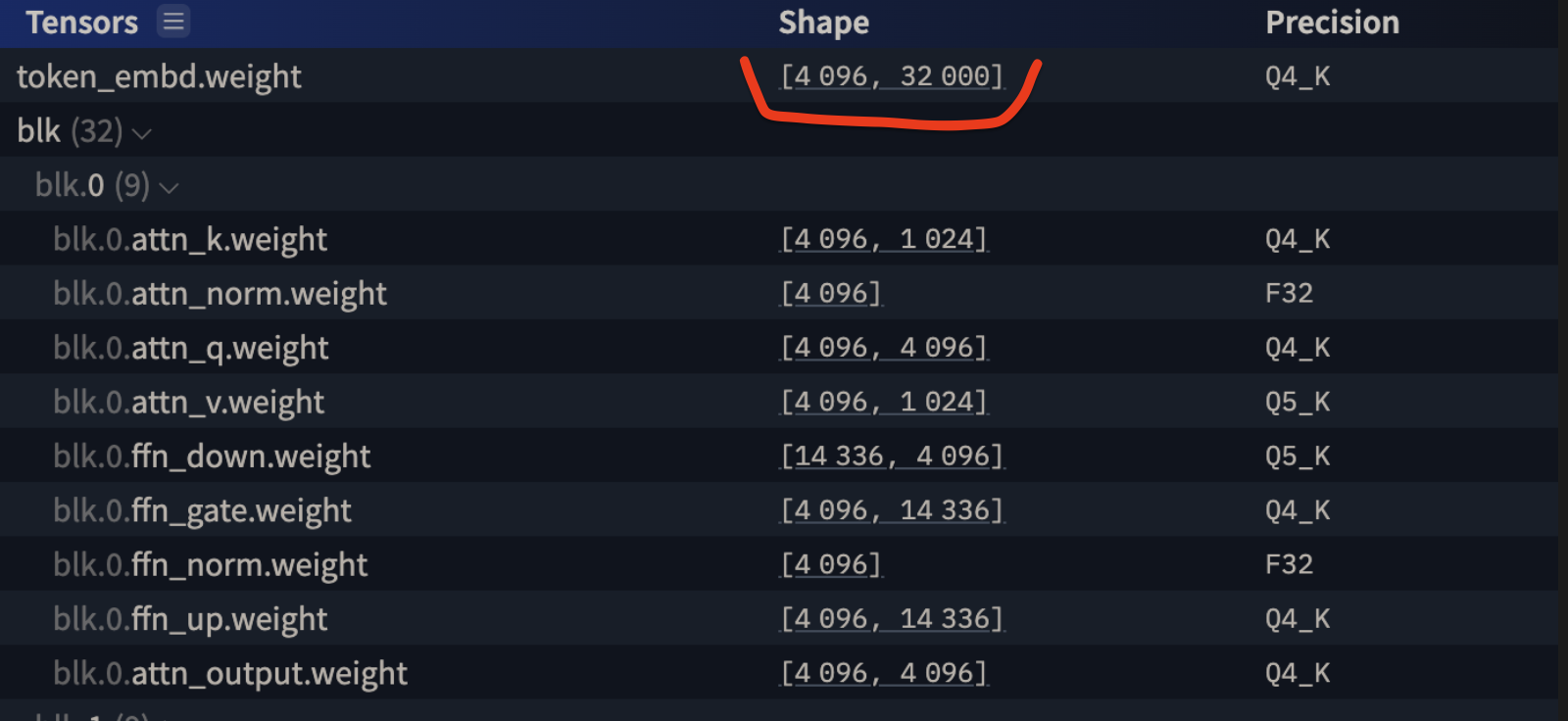
Zaznaczony fragment [4096, 32000] to właśnie macierz embeddingów modelu Bielik w wersji 7B (7 miliardów parametrów). Ma on 32k tokenów w słowniku (czyli 32 tysiące różnych IDków) i każdy z nich jest reprezentowany przez wektor o wymiarze 4096.
Szybka matematyka (przy pomocy hugging face):
- 32000 * 4096 = 131072000 – rozmiar macierzy embeddingów
- w porównaniu do 7B wszystkich parametrów (całego “modelu” jako paczki) to ok 1.81% całości. To miałem na myśli pisząc wcześniej, że macierz embeddingów to relatywnie niewielka część całości 😊
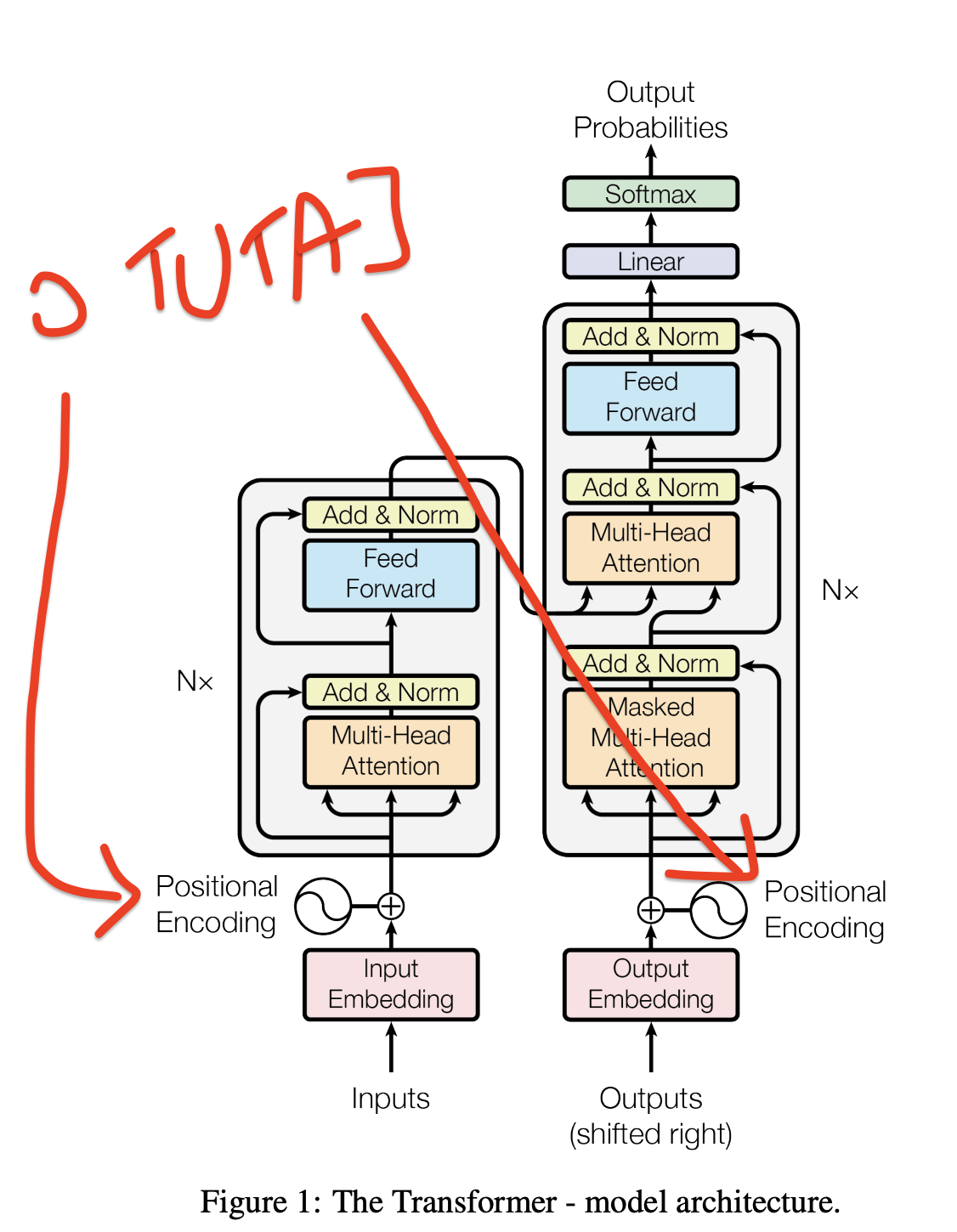
I dalej, Sęk w tym, że kiedy mechanizm atencji będzie potem liczył “bliskość” wektorów do siebie – i będzie to robił ROWNOLEGLE dla WSZYSTKICH wektorów (patrz: GPU 🧑🎨) – to musi pamiętać pozycję danego tokenu w sekwencji.
I to jest rewelacyjna ilustracja tego, jak działają LLMy (i szerzej, Machine Learning) – ktoś znalazł “patent” aby “zakodować” pozycję tokenu w sekwencji do samego wektora. Nie wydłużając jego długości (nie dodając kolejnych wymiarów). Tylko “nakładając” pozycję na istniejące wymiary.
‐ Chcesz powiedzieć, że to nie jest po prostu liczba naturalna (integer) tylko że pozycja jako taka jest wektorem który nakłada się na inny wektor?
‐ Idealnie, dokładnie tak. 👏
I to jest właśnie piękno tych modeli 🤓. Mam nadzieję, że podzielacie moją fascynację ❤️ – to jest piękno matematyki.
Ale ta matematyka jest wyjątkowa i fascynująca poprzez to, co można dzięki tym obliczeniom osiągnąć (to są właśnie “zdolności emergentne“)
Czym jest zatem “nakładanie się” wektorów? Ot, dodawanie wektoru 🤓 pierwszy semestr algebry liniowej.
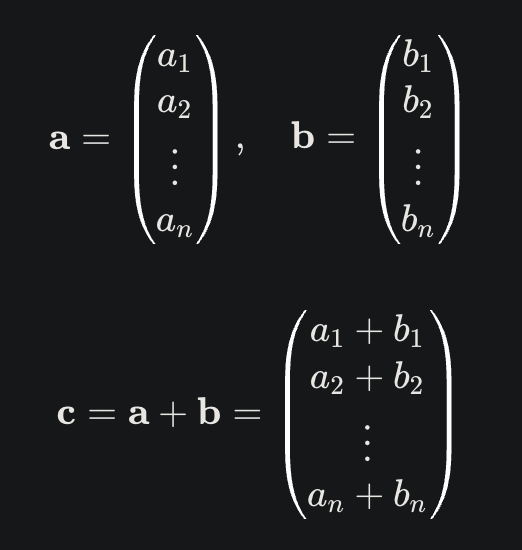
I to jest jedna z najbardziej banalnych operacji, które dostarczają biblioteki typu NumPy, PyTorch czy TensorFlow.
Embedding (osadzenie) należy zatem rozumieć jako – technicznie – zamianę tokenów na wektory liczb (z macierzy embeddingów) i potem “positional encoding”, czyli “nakładanie” na nie wektorów pozycji (z macierzy pozycji).
I dalej – każdy token – a w zasadzie jest spozycjonowany już embedding – będzie dalej płynął po falach GPU i “rozbijał” się o kolejne warstwy tensorów – i na nowo scalał. Ale wtedy już nie będzie reprezentował tokenu, tylko “zinternalizowane” dla modelu przetworzenie. W analogii do ludzkiego mózgu, możemy to próbować porównać do strumienia świadomości: “jabłko” -> “głodny” -> “sklep” -> “kasa” -> “wyskakuj z hajsów”.
Następnie te wektory są “przepuszczane” przez kolejne warstwy modelu (atencja, FFN, atencja, FFN… aż do samego końca):
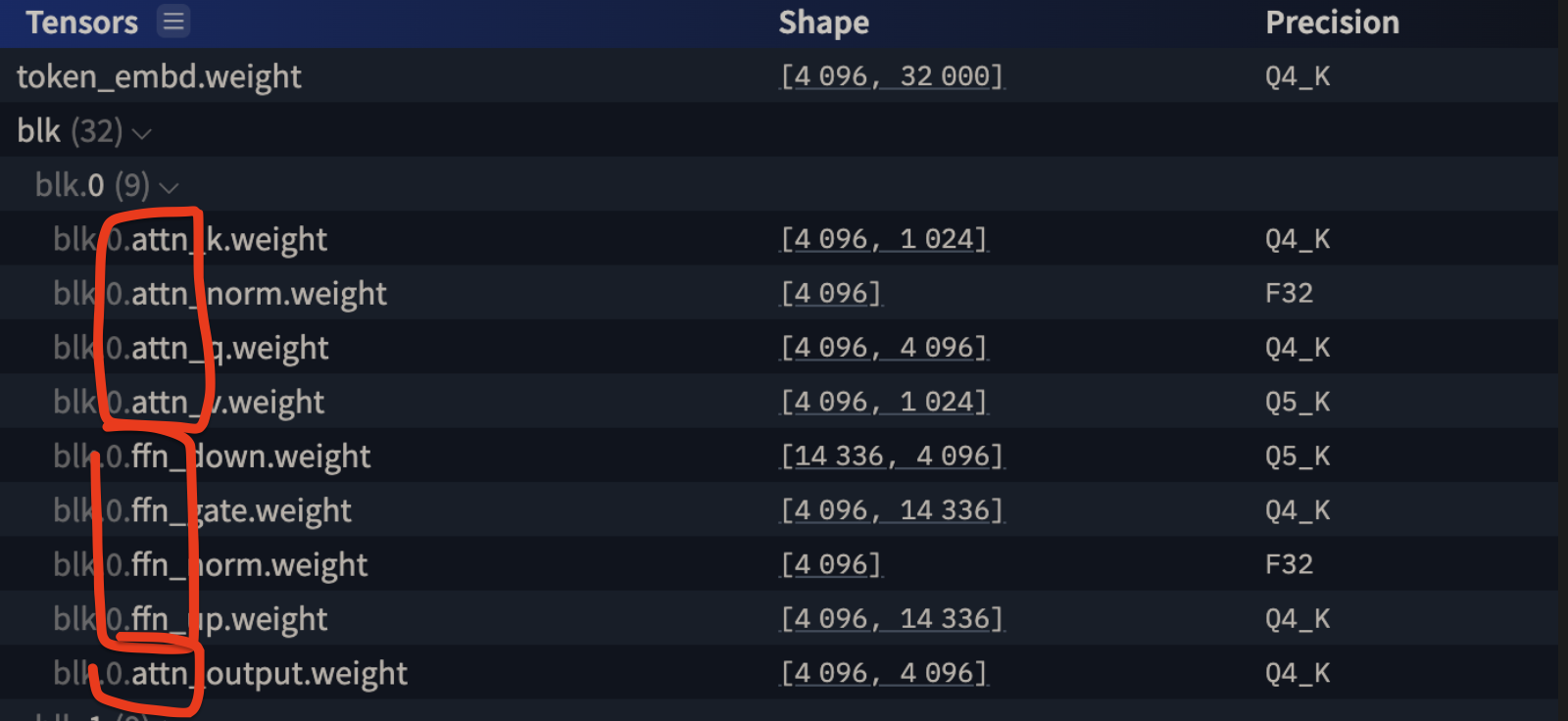
Bielik ma dokładnie 32 warstwy (bloki transformerowe), które działają w nieco podobny sposób, co architektura pipes and filters (nieco podobny 😉), gdzie najpierw jest atencja (czyli wyszukiwanie powiązań między wektorami i “wzmacnianie” ich wartości w “języku modelu”), a potem FFN (feed-forward neural network), która “pogłębia rozumienie”.
Dla przykładu – Atencja składa się, fizycznie, z 3 macierzy (Key, Value i Query) – i one są 2 wymiarowymi tensorami (macierzami):

Ale wszystko (podczas wnioskowania) to są “po prostu operacje na tensorach”. Tylko albo aż.
Totalna magia jest gdzie indziej – w uczeniu maszynowym. I nawet nie w tym, jakie dany “naukowiec” dobrał wzory matematyczne. To, dlaczego wybrano akurat te wzory, i co one docelowo umożliwiają (zdolności emergentne) – to jest właściwa magia.
LLM 🤍♥️ Bielik 🤍♥️ jest, skądinąd, bardzo bliski wzorcowej implementacji architektury Transformers. Co jest rewelacyjne pod kątem nauki – i jednocześnie stawia go z tyłu względem pozostałych modeli, które są już znacznie bardziej zaawansowane.
W następnym odcinku przyjrzymy się kolejnym mechanizmom LLMów 🔥















