Funkcyjna kompozycja w C#

W poprzednim artykule na temat programowania funkcyjnego w C# zajęliśmy się podstawami. Skoro czytasz te słowa, to jest spora szansa, że temat Cię zainteresował! Wejdźmy zatem głębiej w świat programowania funkcyjnego i zajmijmy się składaniem funkcji.

Projekt z kodem źródłowym omawianym w artykule możesz znaleźć tutaj.

Trochę matematyki

Czym jest składanie funkcji i dlaczego jest to takie ważne? Przypomnij sobie lekcje matematyki… Być może pamiętasz, że takie pojęcie się kiedyś w szkole przewinęło. Być może nawet nie jest Ci obcy poniższy zapis:

f ○ g

Złożenie funkcji to nic innego niż wzięcie wyniku jednej funkcji i podanie go jako argument do drugiej funkcji. W matematycznym zapisie:

h = f ○ g
h(x) = g(f(x))

Zwróć uwagę na kolejność. Złożenie f z g polega na wywołaniu najpierw f i podaniu wyniku do g. Ten drugi zapis jest trochę nieintuicyjny, bo czytając od lewej do prawej, najpierw występuje g, a potem f. W C# pozbędziemy się tego problemu.

Dlaczego jest to istotne? Zauważ, że poprzez złożenie f i g powstała nowa funkcja. Dostajemy zatem do ręki narzędzie, dzięki któremu możemy z prostych funkcji budować bardziej złożone. Albo na odwrót, w myśl zasady dziel i rządź, możemy dzielić nasz duży problem na mniejsze, aż dojdziemy do momentu, kiedy problemy są na tyle małe, że realizujemy je za pomocą prostych funkcji. A następnie… składamy te funkcje.

Rysujemy diagramy

Zanim przejdziemy dalej, kilka słów o typach. W szkole rysowało się czasem takie diagramy:

Diagram ten przedstawia w formie obrazkowej funkcję f, która przekształca elementy zbioru X (dziedziny funkcji) na elementy zbioru Y (zbiór wartości). Przykładem takiej funkcji mogłaby być f(x) = x * 2 z całym zbiorem liczb naturalnych jako dziedziną, a zbiorem liczb parzystych jako wartości.

Jeśli przełożymy to na programowanie, to okaże się, że matematyczna definicja funkcji pasuje również tutaj! Zbiory X i Y to nic innego jak typy. X to typ argumentu funkcji (zakładamy, że mówimy o funkcjach jednoargumentowych – w przeciwnym razie stosujemy tzw. currying), a Y to typ zwracanych wartości. Typy to nic innego jak właśnie zbiory dopuszczalnych wartości danej zmiennej.

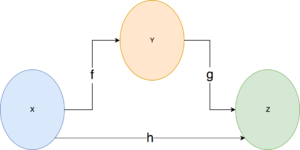
Dzięki takim diagramom możemy w łatwy sposób zobrazować składanie funkcji:

Zwróć uwagę na typy. Funkcja f prowadzi z X do Y, funkcja g z Y do Z. Złożenie f z g prowadzi z X do Z. Skoro zbiory odpowiadają typom, to możemy zastanowić się, jak będzie wyglądać składanie funkcji w C#.

Funkcja Compose

Spróbujmy zapisać sygnaturę funkcji Compose, która przyjmuje dwie funkcje jako argumenty i zwraca funkcję będącą ich złożeniem.

Func<X, Z> Compose<X, Y, Z>(Func<X, Y> f, Func<Y, Z> g)

Funkcja Compose przyjmuje funkcję f, która jest typu Func (przeprowadzającą elementy zbioru X na Y) oraz funkcję g typu Func (przeprowadzającą elementy zbioru Y na Z) i zwraca nową funkcję typu Func. Dokładnie tak jak na diagramie.

Jak wygląda implementacja Compose? Bardzo prosto – dokładnie tak jak matematyczny zapis kilka akapitów wyżej.

public static Func<X, Z> Compose<X, Y, Z>(Func<X, Y> f, Func<Y, Z> g)
{
  return x => g(f(x));
}

Zadeklarowałem tę metodę w statycznej klasie FP. Tam też będziemy dodawać kolejne omawiane funkcje.

Otrzymaliśmy zatem generyczną operację składania funkcji. Za chwilę wykorzystamy ją w praktyce. Wcześniej dodajmy jednak do klasy FP kilka wariantów funkcji Compose różniących się tym ile funkcji składają. Możemy z łatwością utworzyć wariant Compose przyjmujący trzy funkcje:

public static Func<T1, T4> Compose<T1, T2, T3, T4>(Func<T1, T2> f1, Func<T2, T3> f2, Func<T3, T4> f3)
{
  return x => f3(f2(f1(x)));
}

Oraz cztery:

public static Func<T1, T5> Compose<T1, T2, T3, T4, T5>(Func<T1, T2> f1, Func<T2, T3> f2, Func<T3, T4> f3, Func<T4, T5> f4)
{
  return x => f4(f3(f2(f1(x))));
}

Mam nadzieję, że zasada tworzenia kolejnych wariantów jest jasna. Niestety, C# nie umożliwia stworzenia funkcji Compose na tyle ogólnej, żeby mogła operować na dowolnej liczbie argumentów.

Po co to wszystko?

Jeśli jeszcze tu jesteś i powyższe, mocno teoretyczne, paragrafy, Cię nie zniechęciły, to teraz nadchodzi nagroda. Zobaczymy, w jaki sposób wykorzystać składanie funkcji w praktyce!

Zaimplementujemy następujący, dosyć życiowy, scenariusz: dla zadanego symbolu firmy na giełdzie, pobierz notowania akcji z ostatniego miesiąca i znajdź dzień, w którym cena osiągnęła maksimum. Cenę akcji pobierzemy z darmowego API IEX Trading.

Spróbujmy podejść do problemu funkcyjnie. Chcielibyśmy stworzyć funkcję, która dla zadanego symbolu spółki (np. “AAPL” lub “GOOG”) zwróci obiekt zawierający datę oraz cenę akcji, dla dnia z maksymalną ceną. W jaki sposób zaimplementować taką funkcję? Oczywiście, składając ją z prostszych funkcji.

Pomyślmy zatem, na jakie funkcje moglibyśmy rozłożyć powyższą operację.

1. Funkcja przyjmująca napis reprezentujący symbol i zwraca napis zgodny z wymagania API IEX.
2. Funkcja przyjmująca znormalizowany napis zawierający symbol i zwraca napis z JSON-em zawierającym odpowiedź z API IEX.
3. Funkcja przyjmująca napis z JSON-em i zwraca tablicę obiektów reprezentujących notowania.
4. Funkcja przyjmująca tablicę notowań i zwraca obiekt z najwyższym notowaniem.

Udało nam się rozbić problem na złożenie czterech prostych do zaimplementowania funkcji. Zacznijmy od funkcji pierwszej:

Func<string, string> normalizeSymbol = symbol => symbol.ToLower();

Nic nadzwyczajnego – po prostu przekształcamy napis na małe litery. Przyjdźmy zatem do kolejnej funkcji:

var fetchChart = Curry<string, string, string>((period, symbol) =>
{
  using (var httpClient = new HttpClient())
  {
    return httpClient.GetStringAsync($"https://api.iextrading.com/1.0/stock/{symbol}/chart/{period}").Result;
  }
});

Funkcja ta nazywa się fetchChart, ponieważ w nomenklaturze IEX notowania miesięczne określane są jako wykres. Nasza funkcja wysyła zapytanie HTTP pod ustalony URL, dodając jako parametry symbol spółki oraz okres, dla którego pobieramy notowania.

Zauważmy, że funkcja ta jest rozwinięta (curried; więcej o curry’ingu w części pierwszej). Jak już wspomniałem, aby móc składać funkcje, muszą być one jednoargumentowe. Dzięki curry’ingowi sprawiamy, że funkcja fetchChart jest jednoargumentowa.

Pozostałych funkcji nie będziemy definiować, tylko użyjemy funkcji już istniejących.

Składamy funkcje do kupy

Nadszedł wielki moment, w którym to możemy złożyć naszą docelową funkcję.

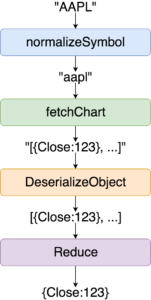
Func<string, ChartItem> getChartItems = Compose(
  normalizeSymbol,
  fetchChart("1m"),
  JsonConvert.DeserializeObject<ChartItem[]>,
  Reduce<ChartItem>((candidate, item) => candidate.Close > item.Close ? candidate : item)
);

Powyższą funkcję możemy oczywiście wywołać w następujący sposób:

var maxDay = getChartItems("AAPL");

Używamy tutaj zdefiniowanej wcześniej funkcji Compose (została zaimportowana z namespace’u FP jako static import, dzięki czemu możemy jej używać w taki sposób). Funkcja ta przyjmuje cztery funkcje i je ze sobą składa. Wyjście każdej funkcji przekazywane jest jako argument kolejnej.

Funkcje normalizeSymbol i fetchChart omówiliśmy sobie już wyżej. Dalej mamy odwołanie do statycznej metody klasy JsonConvert, którą znajdziemy w znanym i lubianym pakiecie NuGet-owym Newtonsoft.Json. Ostatnie wywołanie odwołuje się do funkcji Reduce z namespace’u FP, którą definiujemy poniżej:

public static Func<IEnumerable<T>, T> Reduce<T>(Func<T, T, T> reducer)
{
  return items => items.Aggregate(reducer);
}

Nasz Reduce to nic innego jak opakowanie metody Aggregate z LINQ w taki sposób, aby była curried. Dzięki temu możemy ją wywołać z jednym argumentem i przekazać taką częściowo zaaplikowaną funkcję do Compose. Funkcja ta będzie “czekać” na drugi argument, czyli kolekcję, na której ma się wywołać.

Mam nadzieję, że dostrzegasz piękno takiego zapisu ;-). Rozpisaliśmy zadany problem jako złożenie czterech funkcji. Jest w pełni deklaratywnie, funkcje są czyste, nie ma mutowalnego stanu. Bardzo łatwo zrozumieć co się dzieje patrząc na taki kod.

Warto zauważyć, że w żadnym miejscu w tym kodzie nie musieliśmy utworzyć funkcji anonimowej (wyrażenia lambda). W związku z tym kod nie jest “zanieczyszczony” argumentami funkcji. Taki sposób pisania kodu nazywa się stylem point-free i jest bardzo charakterystyczny dla programowania funkcyjnego.

Podsumowanie

W tym artykule zastosowaliśmy część technik poznanych w części pierwszej. Ponadto zobaczyliśmy, jak ważne jest składanie funkcji w programowaniu funkcyjnym i poznaliśmy jego matematyczne podstawy. Przy okazji zaimplementowaliśmy całkiem życiowy scenariusz w sposób czysto funkcyjny.

Jak Ci się podoba taki styl pisania kodu? Jest bardziej czytelnie?

Ma to dla Ciebie sens? Czy raczej myślisz, że to takie teoretyczne bajanie?

Koniecznie daj znać co myślisz w komentarzach!

Do przeczytania w kolejnej odsłonie cyklu!